Assignment 3: 106 Redux
Due: Wednesday, October 16 at 11:59pm
Submission cutoff: Saturday, October 19 at 11:59pm
In this assignment, you will revisit ghosts of your imperative past: CS 106* assignments, specifically N-grams from 106B and Karel from 106A. You will get experience with different functional programming ideas by recasting these classic assignments into an OCaml setting.
Setup
In the f19-assignments repository, run git pull to get the assignment materials, located in the assign3 directory.
0: OCaml necessities
A few general notes on OCaml that you’ll find useful in complete the assignment. You don’t have to read through all of Section 0 right now, but refer back to here if you’re having a relevant issue.
Named parameters
OCaml allows functions to have named parameters. Named parameters are for two reasons:
- They make the caller-side use of a function more explicit in how parameters are being used. For example, instead of
Map.set m k v, it’sMap.set m ~key:k ~data:v. - They allow a function to be partially applied in any order. For example, I can do
Map.set ~key:kto produce a function that always mapskto a given value, orMap.set ~data:vthat always maps a given key to the valuev.
See below for the syntax of how to use named parameters.
(* Two ways of defining functions with keyword arguments. *)
(* Note that the keyword name is now a part of the function type. *)
let f : a:int -> b:int -> int =
fun ~(a : int) ~(b : int) : int -> a + b
in
let f ~(a : int) ~(b : int) : int =
a + b
in
(* Standard way of calling the function *)
assert ((f ~a:1 ~b:2) = 3);
(* Can provide all arguments at once without keywords *)
assert ((f 1 2) = 3);
(* Can provide keywords in any order *)
assert ((f ~b:2 ~a:1) = 3);
(* Can partially apply the function in any order *)
let f2 = f ~b:1 in
(* Call the function with the remaining keyword *)
assert ((f2 ~a:2) = 3);
(* Can also omit the remaining keyword *)
assert ((f2 2) = 3)
Debugging
An essential part of learning a new language is to understand iterative development—how do you decompose programs, test and debug the pieces, and put it all together? I’ll briefly cover a few different strategies for dealing with compile-time and run-time Ocaml errors.
Compiler errors
In a statically-typed language like OCaml with a complex type system, many of your errors will be caught at compile-time. However, the errors may not always be that interpretable. You should try your best to read the errors and understand them, since the sooner you acquire the skill, the faster your OCaml development will be. For example, let’s say we have this program:
open Core
let main () =
(* bug 1: 0:int is a syntax error *)
(* bug 2: doesn't return an option, returns an int list *)
(* bug 3: doesn't actually sum the list, just returns the last element *)
let buggy_sum (l : int list) : int option =
List.fold_left l ~init:0:int ~f:(fun (acc : int) (n : int) ->
n)
in
assert (buggy_sum [1; 2; 3] = Some 6);
assert (buggy_sum [] = None)
let () = main ()
First, we get the error:
File "src/main.ml", line 5, characters 28-29:
Error: Syntax error
Unfortunately, OCaml’s compiler is awfully unhelpful when it comes to syntax errors. The best thing you can do is look for code with a similar structure, and pattern match off the examples.
List.fold_left l ~init:(0 : int) ~f:(fun (acc : int) (n : int) -> ...
Next, we get the error:
File "src/main.ml", line 5, characters 4-76:
Error: This expression has type int but an expression was expected of type
int option
To understand which expression the error is referring to, we could trace through the characters, but most OCaml IDEs with Merlin equipped will highlight the problematic code stretch. For example, in Emacs, I get:
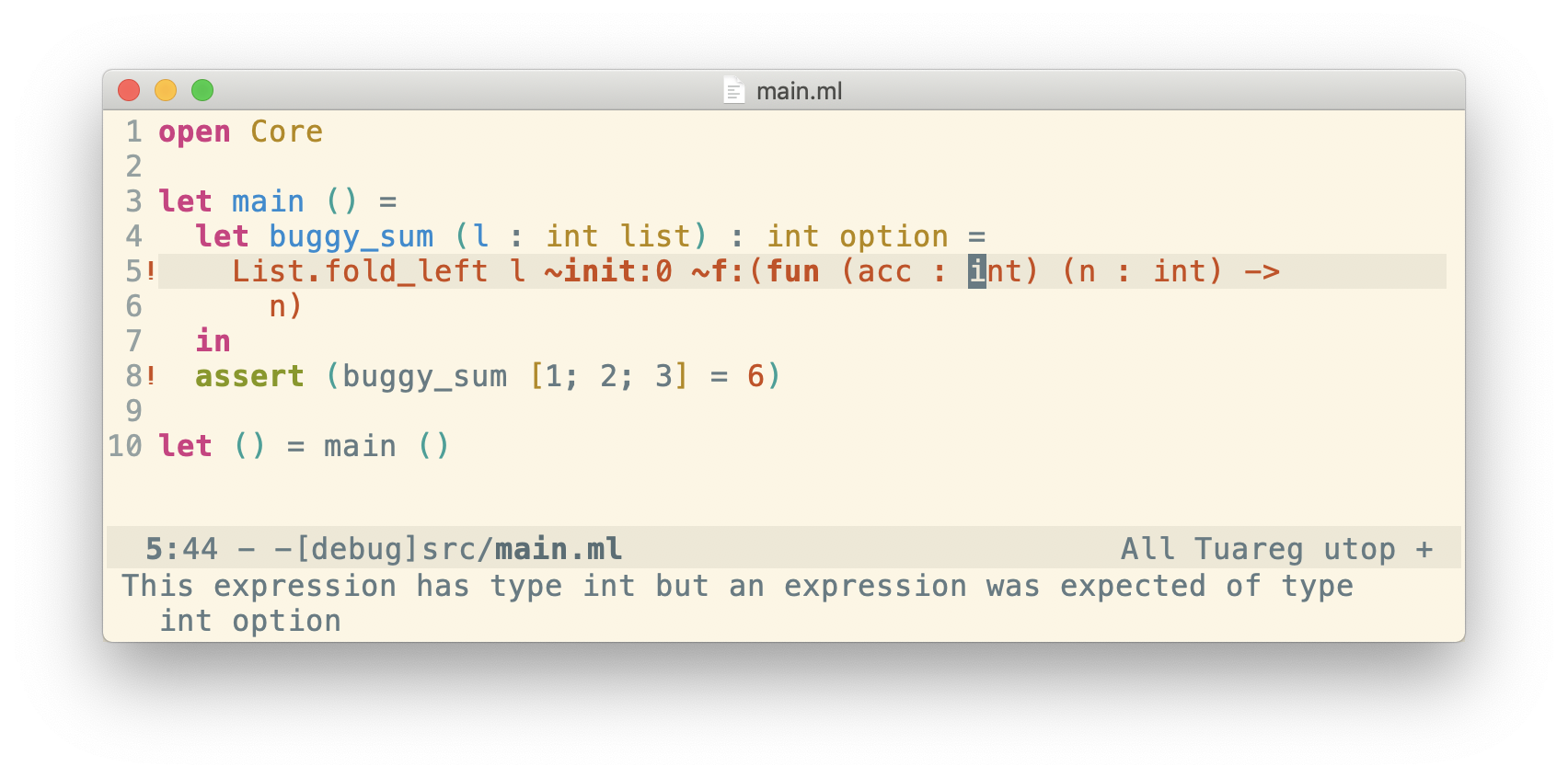
This error says that the entire expression List.fold_left ... returns a value of type int, but it gets back a value of type int option. Generally speaking, you have one of two issues: either the expression is wrong (returning the wrong type), or the expectation is wrong (e.g. the function return type is incorrect). Here, int option is what we want, we need to handle the l = [] case:
match l with
| [] -> None
| _ -> Some (List.fold_left ...)
Printf debugging
The simplest way to debug a runtime error is the time-honored tradition of adding printfs to your code.
List.fold_left l ~init:0 ~f:(fun (acc : int) (n : int) ->
Printf.printf "acc: %d, n: %d\n" acc n;
n)
Then we run the code:
$ make
$ ./main.native
acc: 0, n: 1
acc: 1, n: 2
acc: 2, n: 3
Great, this helps reveal the issue that the accumulator isn’t actually accumulating the sum, just the most recent element. We can then realize the expression n should be n + acc.
ocamldebug
The big downside to printf debugging is that a) you need to know what you should print out, and b) you need a string representation for each value. As an alternative, you can use OCaml’s standard debugger. It’s very poorly documented (this is the best tutorial), but I’ll show you the basics of how it works.
$ make debug
$ ocamldebug ./main.byte
OCaml Debugger version 4.06.1
(ocd) run
Loading program... done.
Time: 99288
Program end.
Uncaught exception: Assert_failure ("src/main.ml", 10, 2)
(ocd) back
Time: 99287 - pc: 2718380 - module Main
10 assert (buggy_sum [1; 2; 3] = Some 6)<|a|>
(ocd) back
Time: 99286 - pc: 2718336 - module Main
10 assert (buggy_sum [1; 2; 3] = Some 6)<|a|>
(ocd) back
Time: 99285 - pc: 2718328 - module Main
10 assert (buggy_sum [1; 2; 3]<|a|> = Some 6)
(ocd) back
Time: 99284 - pc: 2718264 - module Main
8 n))<|a|>
(ocd) back
Time: 99283 - pc: 11136 - module List
110 [] -> <|b|>accu
(ocd) back
Time: 99282 - pc: 11072 - module List
109 <|b|>match l with
(ocd) back
Time: 99281 - pc: 11120 - module List
111 | a::l -> fold_left f (f accu a)<|a|> l
(ocd) back
Time: 99280 - pc: 2718204 - module Main
8 <|b|>n))
(ocd) p n
n: int = 3
(ocd) p acc
acc: int = 2
First, you run make debug to generate a debugger version of the file suffixed with .byte. Then you run ocamldebug <the_binary>.byte which launches the debugger. Typing run will execute the program to completion or until an uncaught exception, like Assert_failure above.
The cool part of ocamldebug is that it’s a time-traveling debugger, meaning unlike gdb, you can step backwards in time to see the state of the past before the exception. Above, we step back until we reach the final evaluation of n inside the fold_left, and use the print (p) command to show the value of each variable.
You can also set a breakpoint on specific lines if you want to stop and inspect program state before reaching an exception:
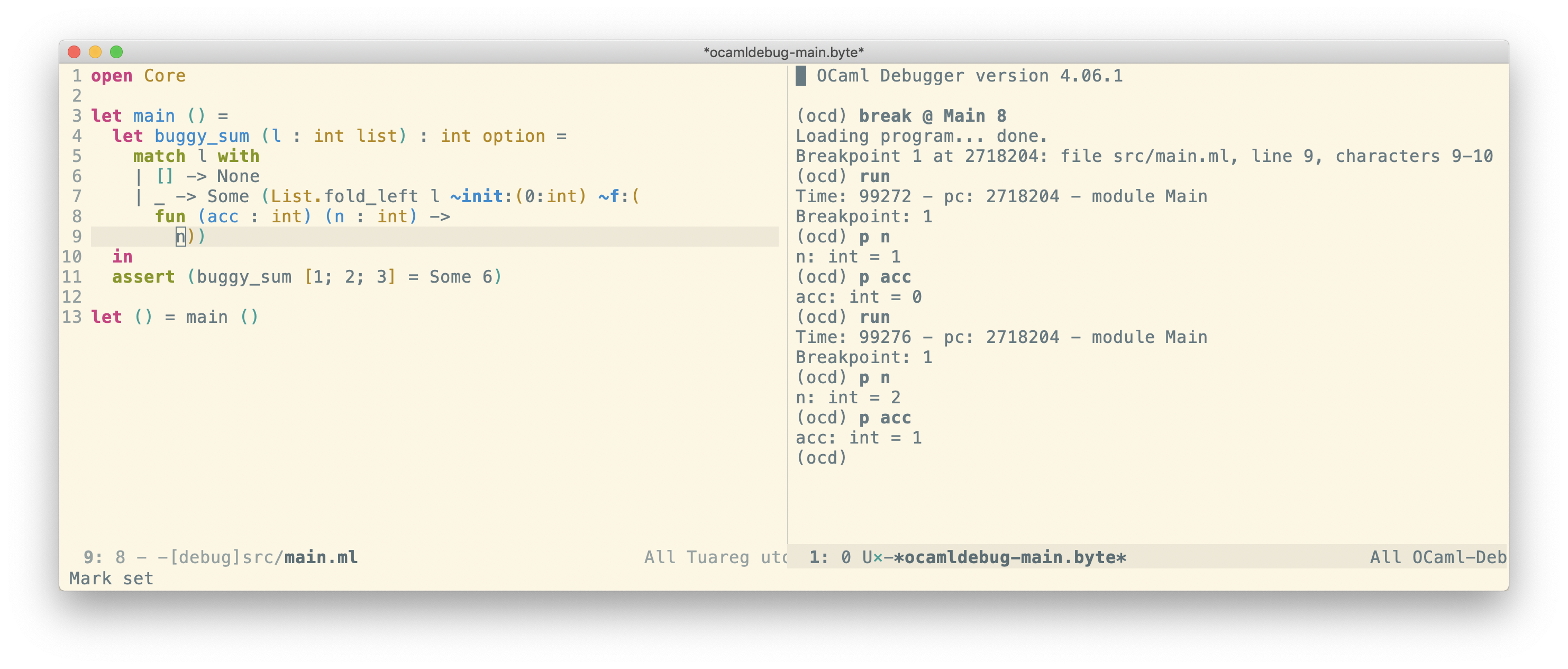
As shown above, Emacs has built-in support for OCaml debug by running M-x ocamldebug. I know at least VSCode also has debug support. IDE integration allows you to see the debugger state and the corresponding source code side by side, unlike the command line where you only see small source code snippets.
1: NGraml (60%)
In CS 106B, the NGrams assignment exercises your knowledge of maps and collections by analyzing a text corpus to build a random text generator. You should read the linked assignment to get a deeper sense of the problem motivation and solution structure. At a high-level, you will decompose a text file into N-grams (subsequences of N words), count the frequency of N-gram suffixes, then sample from the frequency counts as an empirical probability distribution. Your goal is to implement this program in a functional style in OCaml, rather than imperatively using C++. Along the way, you’ll learn about OCaml’s data structures, standard library, and string processing capabilities.
1.1: remove_last (10%)
To start, you will write code to compute all the N-grams in a list of words. You will need a helper function that removes the last element of a list, which we will write a few different ways. Here’s an example of deleting the last element of a linked list in an imperative language (Python):
def remove_last(l):
if l is None:
return None
elif l.next is None:
return None
while l.next is not None:
if l.next.next is None:
l.next = None
break
l = l.next
First, you should translate this into a function remove_last_impl1 that uses recursion instead of loops to traverse the list. Fill in the function at the top of ngram_impl.ml.
remove_last_impl1 : string list -> string list
As a reminder, the basic structure of a recursive list traversal is:
let rec list_traverse (l : string list) : whatever =
match l with
| [] -> (* empty list case *)
| x :: l' -> (* x is the current element, l' is the rest of the list *)
To test your implementation, compile the ngram.native file by running make, then run ./ngram.native hamlet.txt. This will automatically execute any assert expressions in your ngram_impl.ml file. Feel free to add more tests!
Next, you will implement the same function, but without using recursion in remove_last_impl2. Instead, you will use higher order functions. Specifically here, you can use List.filteri which conditionally removes elements of a list. For example, filtering a list to only keep the zero-indexed element as well as odd-numbered elements:
List.filteri [6; 7; 8; 9] ~f:(fun (i : int) (n : int) : bool ->
i = 0 || n mod 2 = 1)
= [6; 7; 9]
Some hints:
- If you introduce variables, either through
letorfun, you should always annotate it with the expected type. This will help avoid getting crazy type errors from OCaml’s type inference engine. - If the input list is empty, then you should return an empty list.
- The “not equals” operator is
<>in OCaml. - You can get the length of a list with
List.length. - The
~f:syntax is used for keyword arguments to functions, meaning arguments with names at the call side instead of just the definition.
1.2: compute_ngrams (12%)
Next, write a function that takes a list of words, and produces all N-grams of those words. (This is essentially a rolling window function.)
compute_ngrams : string list -> int -> string list list
(* For example... *)
compute_ngrams ["a"; "b"; "c"; "d"] 1 = [["a"]; ["b"]; ["c"]; ["d"]]
compute_ngrams ["a"; "b"; "c"; "d"] 2 = [["a"; "b"]; ["b"; "c"]; ["c"; "d"]]
Think about how you would implement this function in an imperative language. Again in Python:
from copy import copy
def compute_ngrams(words, n):
all_ngrams = []
cur_ngram = []
for word in words:
if len(cur_ngram) < n:
cur_ngram.append(word)
else:
all_ngrams.append(copy(cur_ngram))
del cur_ngram[0]
cur_ngram.append(word)
all_ngrams.append(cur_ngram)
return all_ngrams
Your goal is to translate this structure into a functional representation without loops in OCaml. Here, there is a sequential dependency between iterations of the for loop because of cur_ngram. Hence, we need a more general purpose operator, which is essentially the “functional for loop”: fold_left. In a standard for loop, the loop state is implicit, meaning variables like all_ngrams are loop state by virtue of being used in the loop. By contrast, functional loops have explicit state. For example, to add all the elements of a list:
(List.fold_left [1; 2; 3] ~init:0 ~f:(fun (accum : int) (n : int) : int -> accum + n)) = 6
The fold_left function runs the input f with an initial state of init, and then accumulates the state on each call. So here, the sum is computed as (f (f (f 0 1) 2) 3). For compute_ngrams, you will need to think about: what is your list state? And how will you emulate the logic for changing cur_ngram on each loop? Some hints:
- You can assume
n > 0and(List.length l) >= n. - Remember that the “cons” operator
x :: lputs the elementxat the beginning of listl. - You may find the
List.revfunction useful for reversing a list. - In general, don’t worry too much about inefficiencies or computational complexity. However, if your script is so slow to the point that it does not finish within a second or two, you may need to revisit your design decisions.
- If you want a particular challenge, see if you can implement this function without using any new
funfunctions. Meaning build the N-grams solely out of standard library functions and function combinators.
1.3: ngram_map (10%)
Now that we can compute N-grams in a document, the next step is to build a data structure that maps (N-1)-grams to a list of observed suffix words. See “Algorithm Step 1” of the CS 106B handout for an extremely useful visualization.

We will represent the map data structure using a Map from N-grams to word lists. (The Map.Poly stands for “polymorphic comparison on keys”, meaning the implementation is slightly slower than e.g. String.Map that is specialized for string keys).
type ngram = string list
type ngram_map = (ngram, string list) Map.Poly.t
Your task is to define a small API around the ngram_map type. Specifically, you first will implement the function to construct an ngram_map:
ngram_map_add : ngram_map -> ngram -> ngram_map
(* For example... *)
ngram_map_add {["a"; "b"] -> ["c"]} ["a";"b";"d"] = {["a";"b"] -> ["c";"d"]}
ngram_map_add {["a"; "b"] -> ["c"]} ["a";"c";"d"] = {["a";"b"] -> ["c"], ["a";"c"] -> ["d"]}
(Note that the {k -> v} notation is not real OCaml code. It’s just used here to denote a dictionary literal for notational convenience.)
You will find the following functions useful:
List.split_n: partitions a list into two pieces at the indexn, e.g.List.split_n [1; 2; 3] 1 = ([1], [2; 3])Map.Poly.find: returnsSome(v)if a keykis in the map, andNoneotherwise, e.g.Map.Poly.find {1 -> "a"} 1 = Some "a" Map.Poly.find {1 -> "a"} 2 = NoneMap.Poly.set: sets a key to a value in the map, e.g.Map.Poly.set {1 -> "a"} ~key:2 ~data:"b" = {1 -> "a"; 2 -> "b"}
Briefly, an extended example of using the Map.Poly data structure.
(* The type of a map is (key, value) Map.Poly.t.
* An empty map is Map.Poly.empty. *)
let m : (int, string) Map.Poly.t = Map.Poly.empty in
(* We can use the set and find functions as described above. *)
let m = Map.Poly.set m ~key:1 ~data:"a" in
assert (Map.Poly.find m 1 = Some "a")
assert (Map.Poly.find m 2 = None)
1.4: word_distribution (18%)
Once our N-gram map is constructed, the next step is to turn the word lists into probability distributions that we can sample from. Specifically, a probability distribution over a discrete set of words is a map from strings to floats:
type word_distribution = float String.Map.t
(* For example... *)
{"a" -> 0.3, "b" -> 0.7}
Your goal is to implement two functions, one to compute a distribution from an N-gram map, and one to sample from a distribution.
ngram_map_distribution : ngram_map -> ngram -> word_distribution option
(* For example... *)
ngram_map_distribution {["a";"b"] -> ["c";"c";"d"]} ["a";"b"] = {"c" -> 0.66; "d" -> 0.33}
sample_distribution : word_distribution -> string
Some hints:
ngram_map_distributionshould returnNoneif the requestedngramdoes not exist in the map.- If you want a clever way to turn a word list into a distribution, take a look at String.Map.of_alist_reduce.
- You can use
float_of_intto turn an integer into a float. - You can use
Random.float 1.to produce a random float between 0 and 1. - Like lists, you can use
String.Map.foldto iterate over all the key-value pairs of a word distribution in a for-loop style.
1.5: sample_n (10%)
Finally, you need to define a function sample_n that takes as input a starting ngram, and then randomly samples up to n words following the strategy in Algorithm Step 2 of the CS 106B handout. If the requested ngram (or any subsequent generated ngram along the way) does not exist in the map, you may immediately stop and return fewer than n words.
sample_n : ngram_map -> ngram -> int -> string list
At last, if you run ./ngram.native hamlet.txt you should finally see the random output!
$ ./ngram.native hamlet.txt
When in one line two crafts directly meet. This man shall end his part in peace; the clown shall make
Or applied to the introduction of the Homotopy Type Theory book:
$ ./ngram.native hott.txt -ngram 2 -nwords 30
and essentially sets and notation, and a taste of (countable) choice can be more powerful when faced with
inductively defined type theory from the working mathematician. This chapter is now
2: KarelVM (40%)
In CS 106A, Karel is an introduction to programming assignment. You use a small set of commands and predicates along with a subset of Java to move a little robot around a grid, performing various beeper-related tasks. The Karel coursereader explains everything in greater detail.
Deeply uninspired by the use of Java, you decide to implement your own Karel bytecode and interpreter in OCaml, collectively the Karel Virtual Machine (or KarelVM). This will give you experience in using OCaml’s algebraic data types, as well as interpreting a miniature domain-specific language.
First, we define the type of the world’s state:
type cell = Empty | Wall | Beeper
type grid = cell list list
type dir = North | West | South | East
type pos = int * int
type state = {
karel_pos : pos;
karel_dir : dir;
grid : grid;
}
A Karel world is described by a state record containing Karel’s position and direction, along with a 2D grid of cells. Each cell is either empty, or it contains a wall or a beeper. (For simplicity, we do not distinguish between corners and walls, but rather just have a generic notion of grid cells.) Karel can be facing either north, south, east, or west, and a position is an index (i, j) in this grid. For example, this state:
let s : state = {
karel_pos = (0, 1);
karel_dir = North;
grid = [[Empty; Empty; Wall]; [Empty; Wall; Wall]; [Empty; Beeper; Empty]]
}
Could be visualized as:
. . x
K x x
. B .
Where . is empty, x is a wall, K is Karel, and B is a beeper. We use (0, 0) as the top left of the grid.
2.1: state_to_string (5%)
More broadly, this methodology is common in functional programming: we first define our data types that establish the shape of the application domain. Then we define methods (like to_string) to visualize the data, helping us debug as we implement the actions/behavior on the data. Hence, we’ll start by defining a function state_to_string that converts a state record to a string following the rules above.
state_to_string : state -> string
You can test your solution on Karel’s problem 1 grid by running:
$ ./karel.native problem1
Initial state:
. . . . . . .
. x x x x x .
. x K . . x .
. x . . . . B
. x x x x x .
. . . . . . .
Fill in your implementation in the karel_impl.ml file.
A few notes:
- You should use the precise convention/format described above. You do not need to visualize Karel’s direction. If Karel and a beeper share the same square, put a
Kinstead ofB. - The
gridis laid out with the northwest corner at (0, 0) and the southeast corner at (width, height). - You will find the following functions useful:
String.concat: concatenates a list of strings into a single string. For example:String.concat ~sep:"," ["a"; "b"; "c"] = "a,b,c"List.mapi: transforms a list by applying a function to each element. The function takes as input the element’s index and value. For example:List.mapi [5; 2; 4] ~f:(fun (i : int) (n : int) : int -> (i, n+1)) = [(0, 6), (1, 3), (2, 5)]
- You should apply the same iterative development methodology in creating this function that you would in any other language or context. For example, start by taking the grid and turning it into a string grid of only
'.'of the same size. Then change the cell character based on the grid cell. Then add Karel’s position into the grid. Write tests and debug along the way—do not write the whole function in one go!
2.2: eval_pred (10%)
Next, we want to be able to answer a fixed set of questions (predicates) about our world state. Specifically, you will implement a function eval_pred that takes a state and a predicate, returning a whether the predicate is true or not.
type predicate =
| FrontIs of cell
| NoBeepersPresent
| Facing of dir
| Not of predicate
eval_pred : state -> predicate -> bool
Each predicate’s specification:
FrontIs cell: returns true if the cell in front of Karel has the same type ascell. Also returns true if Karel’s front is out of bounds andcell = Wall.NoBeepersPresent: returns true if Karel’s current cell does not contain a beeper.Facing dir: returns true if Karel is facing the directiondir.Not p: returns the negation of the predicatep.
To implement these predicates, you will need the get_cell helper function. For example, using the 3x3 grid state from before:
get_cell s (0, 0) = Some Empty
get_cell s (1, 1) = Some Wall
get_cell s (-1, 0) = None
get_cell s (0, 5) = None
2.3: step (17%)
Next, you will implement the core routine of the virtual machine that evaluates a single instruction and changes the grid state accordingly. Specifically, we have six instructions:
type instruction =
| Move
| TurnLeft
| PickBeeper
| PutBeeper
| While of predicate * instruction list
| If of predicate * instruction list * instruction list
step : state -> instruction -> state
The first four instructions are Karel’s canonical API: move, turn left, pick up a beeper, and put down a beeper (you can assume Karel always has infinite beeper supply and capacity). The next two emulate Java statements within the KarelVM: a while loop executes an instruction list while the predicate is true, and an if statement executes one of two instruction lists based on the predicate. For example, we can set up Karel’s Problem 1 on the following grid:
. . . . . . .
. x x x x x .
. x K . . x .
. x . . . . B
. x x x x x .
. . . . . . .
Then an instruction sequence to fetch the beeper and return Karel to its original position/direction looks like:
[Move; Move; TurnLeft; TurnLeft; TurnLeft;
Move; TurnLeft;
Move; Move; PickBeeper; TurnLeft; TurnLeft;
Move; Move; Move; Move; TurnLeft; TurnLeft; TurnLeft;
Move; TurnLeft; TurnLeft; TurnLeft;
Your task is to implement the step function to emulate Karel’s behavior on the grid. step takes as input the current state and an instruction, and it returns the new state after executing the instruction.
Elaborating on the semantics of each instruction:
Move: this should move Karel one square forward in Karel’s current direction. If the front square is a wall, then this operation does nothing.TurnLeft: this turns Karel 90 degrees to the left. (e.g. North -> West)PickBeeper: this picks a beeper from Karel’s current cell. If the cell does not contain a beeper, this operation does nothing.PutBeeper: this puts a beeper into Karel’s current cell. If the cell already contains a beeper, this operation does nothing.While(pred, instrs): while the predicatepredis true, execute each instruction in theinstrslist.If(pred, then_, else_): if the predicatepredis true, then execute thethen_instructions, else execute theelse_instructions.
Some more notes on implementing step:
- If you’re getting weird unsolvable type or syntax errors, make sure to put parentheses around nested match expressions. For example if you have something like:
match foo of | X -> match bar of | A -> .. | B -> .. | Y -> ..There is a syntactic ambiguity where the parser doesn’t know if the
B -> ...case belongs to thefoomatch or thebarmatch. Instead, add parentheses:match foo of | X -> (match bar of | A -> .. | B -> ..) | Y -> .. - You can perform a concise functional update on a record (meaning change one field and leave the rest the same) like so:
let state : state = { ... } in let new_state = {state with karel_pos = (0, 0)} in ... - You may find it useful to add a mutually recursive function with
step. For example, we’ve already defined one calledstep_listthat foldsstepover a list of instructions. The idea behind the mutual recursion is thatstepis allowed to callstep_list(e.g. if you’re executing aniforwhile), andstep_listis allowed to callstep. - To change a a cell in the grid, we have provided a helper function to do so:
set_cell : grid -> point -> cell -> grid
2.4: checkers_algo (8%)
Finally, your goal is to implement the checkerboard algorithm for Problem 3 of the Karel assignment using this domain-specific language. Specifically, Karel starts facing east at (0, 0) on an grid of arbitrary size. For simplicity, you can assume that . Then Karel should lay down beepers in a checkboard pattern starting from the origin. For example:
$ ./karel.native problem3 -m 4 -n 7
Final state:
B . B . B . B
. B . B . B .
B . B . B . B
K B . B . B .
You should put your algorithm into the checkers_algo variable at the bottom of karel_impl.ml
checkers_algo : instruction list
- You cannot change or extend the instruction set in anyway.
- Your algorithm should terminate only once the entire grid has been checkered.
- Karel can finish in any position or orientation.
- The reference solution contains 32 primitive instructions and 7 if/whiles (all at various levels of nesting). Kudos if you can come up with a more concise solution!
Submission
Run ./make_submission.sh and upload the newly created assign3.zip file to the gradescope assignment.